Point in Polygon & Intersect¶
Finding out if a certain point is located inside or outside of an area, or finding out if a line intersects with another line or polygon are fundamental geospatial operations that are often used e.g. to select data based on location. Such spatial queries are one of the typical first steps of the workflow when doing spatial analysis. Performing a spatial join (will be introduced later) between two spatial datasets is one of the most typical applications where Point in Polygon (PIP) query is used.
How to check if point is inside a polygon?¶
Computationally, detecting if a point is inside a polygon is most commonly done using a specific formula called Ray Casting algorithm. Luckily, we do not need to create such a function ourselves for conducting the Point in Polygon (PIP) query. Instead, we can take advantage of Shapely’s binary predicates that can evaluate the topolocical relationships between geographical objects, such as the PIP as we’re interested here.
There are basically two ways of conducting PIP in Shapely:
- using a function called .within() that checks if a point is within a polygon
- using a function called .contains() that checks if a polygon contains a point
Notice: even though we are talking here about Point in Polygon operation, it is also possible to check if a LineString or Polygon is inside another Polygon.
- Let’s first create a Polygon using a list of coordinate-tuples and a couple of Point objects
from shapely.geometry import Point, Polygon
# Create Point objects
p1 = Point(24.952242, 60.1696017)
p2 = Point(24.976567, 60.1612500)
# Create a Polygon
coords = [(24.950899, 60.169158), (24.953492, 60.169158), (24.953510, 60.170104), (24.950958, 60.169990)]
poly = Polygon(coords)
# Let's check what we have
In [1]: print(p1)
POINT (24.952242 60.1696017)
In [2]: print(p2)
�����������������������������POINT (24.976567 60.16125)
In [3]: print(poly)
��������������������������������������������������������POLYGON ((24.950899 60.169158, 24.953492 60.169158, 24.95351 60.170104, 24.950958 60.16999, 24.950899 60.169158))
- Let’s check if those points are
withinthe polygon
# Check if p1 is within the polygon using the within function
In [4]: p1.within(poly)
Out[4]: True
# Check if p2 is within the polygon
In [5]: p2.within(poly)
�������������Out[5]: False
Okey, so we can see that the first point seems to be inside that polygon and the other one doesn’t.
- In fact, the first point is close to the center of the polygon as we can see:
# Our point
In [6]: print(p1)
POINT (24.952242 60.1696017)
# The centroid
In [7]: print(poly.centroid)
�����������������������������POINT (24.95224242849236 60.16960179038188)
- It is also possible to do PIP other way around, i.e. to check if polygon contains a point:
# Does polygon contain p1?
In [8]: poly.contains(p1)
Out[8]: True
# Does polygon contain p2?
In [9]: poly.contains(p2)
�������������Out[9]: False
Thus, both ways of checking the spatial relationship results in the same way.
Which one should you use then? Well, it depends:
if you have many points and just one polygon and you try to find out which one of them is inside the polygon:
- you need to iterate over the points and check one at a time if it is within() the polygon specified
if you have many polygons and just one point and you want to find out which polygon contains the point
- you need to iterate over the polygons until you find a polygon that contains() the point specified (assuming there are no overlapping polygons)
Intersect¶
Another typical geospatial operation is to see if a geometry intersect or touches another one. The difference between these two is that:
- if objects intersect, the boundary and interior of an object needs to intersect in any way with those of the other.
- If an object touches the other one, it is only necessary to have (at least) a single point of their boundaries in common but their interiors shoud NOT intersect.
Let’s try these out.
- Let’s create two LineStrings
from shapely.geometry import LineString, MultiLineString
# Create two lines
line_a = LineString([(0, 0), (1, 1)])
line_b = LineString([(1, 1), (0, 2)])
- Let’s see if they intersect
In [10]: line_a.intersects(line_b)
Out[10]: True
- Do they also touch each other?
In [11]: line_a.touches(line_b)
Out[11]: True
Indeed, they do and we can see this by plotting the features together
# Create a MultiLineString
In [12]: multi_line = MultiLineString([line_a, line_b])
In [13]: multi_line
Out[13]: <shapely.geometry.multilinestring.MultiLineString at 0x20c9f086a20>
Thus, the line_b continues from the same node ( (1,1) ) where line_a ends.
However, if the lines overlap fully, they don’t touch due to the spatial relationship rule, as we can see:
- Check if line_a touches itself
# Does the line touch with itself?
In [14]: line_a.touches(line_a)
Out[14]: False
- It does not. However, it does intersect
# Does the line intersect with itself?
In [15]: line_a.intersects(line_a)
Out[15]: True
Point in Polygon using Geopandas¶
Next we will do a practical example where we check which of the addresses from previous tutorial are located in Southern district of Helsinki. Let’s start by downloading a KML-file that has the Polygons for districts of Helsinki Region (data openly available from Helsinki Region Infoshare).
- Let’s start by reading the addresses from the Shapefile that we saved earlier.
import geopandas as gpd
fp = "/home/geo/addresses.shp"
data = gpd.read_file(fp)
Reading KML-files in Geopandas¶
It is possible to read the data from KML-file in a similar manner as Shapefile. However, we need to first, enable the KML-driver which is not enabled by default (because KML-files can contain unsupported data structures, nested folders etc., hence be careful when reading KML-files).
- Let’s enable the read and write functionalities for KML-driver by passing
'rw'to whitelist of fiona’s supported drivers:
In [16]: import geopandas as gpd
In [17]: import matplotlib.pyplot as plt
In [18]: gpd.io.file.fiona.drvsupport.supported_drivers['KML'] = 'rw'
Now we should be able to read a KML file with Geopandas.
- Let’s read the data from a following KML -file:
# Filepath to KML file
fp = "/home/geo/PKS_suuralue.kml"
In [19]: polys = gpd.read_file(fp, driver='KML')
In [20]: polys
Out[20]:
Name Description \
0 Suur-Espoonlahti
1 Suur-Kauklahti
2 Vanha-Espoo
3 Pohjois-Espoo
4 Suur-Matinkylä
5 Kauniainen
6 Suur-Leppävaara
7 Suur-Tapiola
8 Myyrmäki
9 Kivistö
10 Eteläinen
11 Kaakkoinen
12 Keskinen
13 Läntinen
14 Pohjoinen
15 Koillinen
16 Aviapolis
17 Tikkurila
18 Koivukylä
19 Itäinen
20 Östersundom
21 Hakunila
22 Korso
geometry
0 POLYGON Z ((24.775059677807 60.1090604462157 0...
1 POLYGON Z ((24.6157775254076 60.1725681273527 ...
2 POLYGON Z ((24.6757633262026 60.2120070032819 ...
3 POLYGON Z ((24.767921197401 60.2691954732391 0...
4 POLYGON Z ((24.7536131356802 60.1663051341717 ...
5 POLYGON Z ((24.6907528033566 60.2195779731868 ...
6 POLYGON Z ((24.797472695835 60.2082651196077 0...
7 POLYGON Z ((24.8443596422129 60.1659790707387 ...
8 POLYGON Z ((24.8245867448802 60.2902531157585 ...
9 POLYGON Z ((24.9430919106369 60.3384471629062 ...
10 POLYGON Z ((24.7827651307035 60.09997268858 0,...
11 POLYGON Z ((24.8480782099727 60.0275589731893 ...
12 POLYGON Z ((24.9085548098731 60.2082029641503 ...
13 POLYGON Z ((24.832174555671 60.2516121985945 0...
14 POLYGON Z ((24.8992644865152 60.2689368800439 ...
15 POLYGON Z ((24.9722813313308 60.2432476462193 ...
16 POLYGON Z ((24.9430919106369 60.3384471629062 ...
17 POLYGON Z ((24.9764047156358 60.2896890295612 ...
18 POLYGON Z ((24.9942315864552 60.3329637072809 ...
19 POLYGON Z ((25.0351655840904 60.23627484214 0,...
20 POLYGON Z ((25.233518559787 60.2565486562817 0...
21 POLYGON Z ((25.0847165922124 60.2724847557756 ...
22 POLYGON Z ((25.1238010972777 60.341907177167 0...
Nice, now we can see that we have 22 districts in our area. We are interested in an area that is called Eteläinen (‘Southern’ in english).
- Let’s select that one and see where it is located, and plot also the points on top of the map.
In [21]: southern = polys.ix[polys['Name']=='Eteläinen']
In [22]: southern.reset_index(drop=True, inplace=True)
In [23]: fig, ax = plt.subplots()
In [24]: polys.plot(ax=ax, facecolor='gray');
In [25]: southern.plot(ax=ax, facecolor='red');
In [26]: data.plot(ax=ax, color='blue', markersize=5);
In [27]: plt.tight_layout();
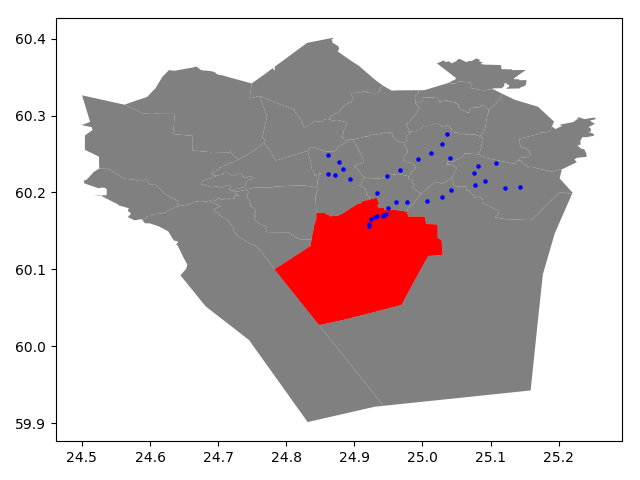
Okey, so we can see that, indeed, certain points are within the selected red Polygon.
Let’s find out which one of them are located within the Polygon. Hence, we are conducting a Point in Polygon query.
- Let’s first enable shapely.speedups which makes some of the spatial queries running faster.
In [28]: import shapely.speedups
In [29]: shapely.speedups.enable()
- Let’s check which Points are within the
southernPolygon. Notice, that here we check if the Points arewithinthe geometry of thesouthernGeoDataFrame. Hence, we use theloc[0, 'geometry']to parse the actual Polygon geometry object from the GeoDataFrame.
In [30]: pip_mask = data.within(southern.loc[0, 'geometry'])
In [31]: print(pip_mask)
0 True
1 True
2 False
3 False
4 True
5 False
6 False
7 False
8 False
9 False
10 True
11 False
12 False
13 False
14 False
15 False
16 False
17 False
18 False
19 False
20 False
21 False
22 False
23 False
24 False
25 False
26 False
27 False
28 False
29 False
30 True
31 True
32 True
33 True
34 False
dtype: bool
As we can see, we now have an array of boolean values for each row, where the result is True
if Point was inside the Polygon, and False if it was not.
- We can now use this mask array to select the Points that are inside the Polygon. Selecting data with this kind of mask array (of boolean values) is
easy by passing the array inside the
locindexing function of Pandas.
In [32]: pip_data = data.loc[pip_mask]
In [33]: pip_data
Out[33]:
address id \
0 Kampinkuja 1, 00100 Helsinki, Finland 1001
1 Kaivokatu 8, 00101 Helsinki, Finland 1002
4 Tyynenmerenkatu 9, 00220 Helsinki, Finland 1005
10 Rautatientori 1, 00100 Helsinki, Finland 1011
30 Urho Kekkosen katu 1, 00100 Helsinki, Finland 1031
31 Gräsviksgatan 17, 00101 Helsingfors, Finland 1032
32 Stillahavsgatan 3, 00220 Helsingfors, Finland 1033
33 Vilhelmsgatan 4, 00101 Helsingfors, Finland 1034
geometry
0 POINT (24.9301701 60.1683731)
1 POINT (24.9418933 60.1698665)
4 POINT (24.9214846 60.1565781)
10 POINT (24.94251 60.1711874)
30 POINT (24.9337569 60.1694809)
31 POINT (24.9250072 60.16500139999999)
32 POINT (24.9214046 60.159069)
33 POINT (24.9468514 60.1719108)
Let’s finally confirm that our Point in Polygon query worked as it should by plotting the data.
In [34]: southern = polys.ix[polys['Name']=='Eteläinen']
In [35]: southern.reset_index(drop=True, inplace=True)
In [36]: fig, ax = plt.subplots()
In [37]: polys.plot(ax=ax, facecolor='gray');
In [38]: southern.plot(ax=ax, facecolor='red');
In [39]: pip_data.plot(ax=ax, color='gold', markersize=2);
In [40]: plt.tight_layout();
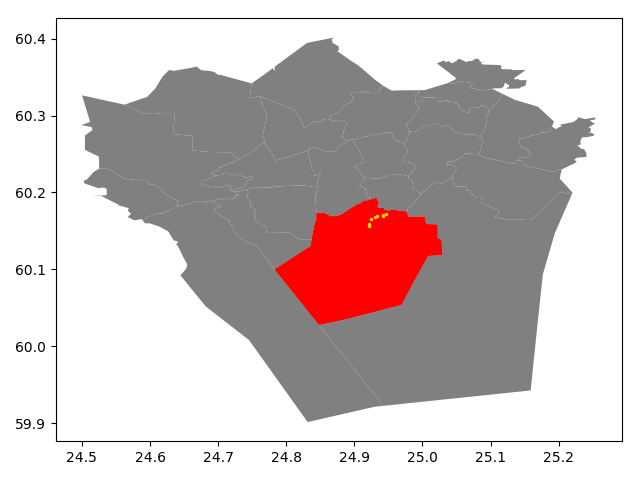
Perfect! Now we only have the (golden) points that, indeed, are inside the red Polygon which is exactly what we wanted!