Geometric operations¶
Overlay analysis¶
The aim here is to make an overlay analysis where we select only specific polygon cells from the data based on the borders of municipality of Helsinki.
Let’s first read the data.
import geopandas as gpd
import matplotlib.pyplot as plt
import shapely.speedups
# Let's enable speedups to make queries faster
shapely.speedups.enable()
# File paths
border_fp = "/home/geo/data/Helsinki_borders.shp"
grid_fp = "/home/geo/data/TravelTimes_to_5975375_RailwayStation.shp"
# Read files
grid = gpd.read_file(grid_fp)
hel = gpd.read_file(border_fp)
Let’s check that the coordinate systems match.
In [1]: hel.crs
Out[1]: {'init': 'epsg:3067'}
In [2]: grid.crs
������������������������������Out[2]: {'init': 'epsg:3067'}
Indeed, they do. This is pre-srequisite to conduct spatial operations between the layers (as their coordinates need to match).
Let’s see how our datasets look like. We will use the Helsinki municipality layer as our basemap and plot the other layer on top of that.
In [3]: basemap = hel.plot()
In [4]: grid.plot(ax=basemap, facecolor='gray' linewidth=0.02);
# Use tight layout
Let’s do an overlay analysis and select polygons from grid that intersect with our Helsinki layer.
Note
This can be a slow procedure with less powerful computer. There is a way to overcome this issue by doing the analysis in batches which is explained below, see the performance-tip.
In [5]: result = gpd.overlay(grid, hel, how='intersection')
Let’s plot our data and see what we have.
In [6]: result.plot(color="b")
Out[6]: <matplotlib.axes._subplots.AxesSubplot at 0x2ce1cb682b0>
In [7]: plt.tight_layout()
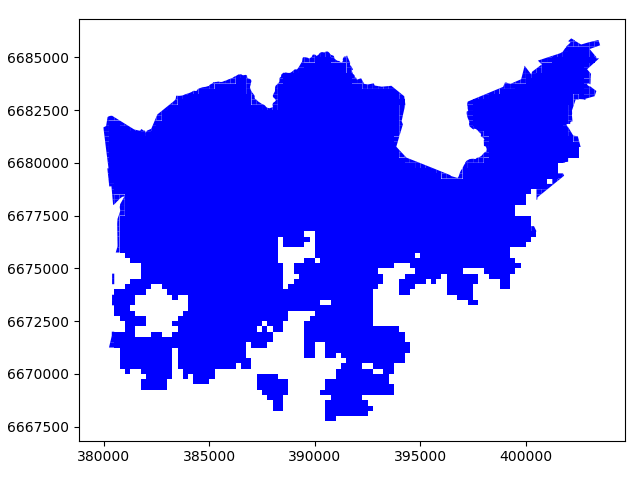
Cool! Now as a result we have only those grid cells included that intersect with the Helsinki borders and the grid cells are clipped based on the boundary.
Whatabout the data attributes? Let’s see what we have.
In [8]: result.head()
Out[8]:
car_m_d car_m_t car_r_d car_r_t from_id pt_m_d pt_m_t pt_m_tt \
0 15981 36 15988 41 6002702 14698 65 73
1 16190 34 16197 39 6002701 14661 64 73
2 15727 33 15733 37 6001132 14256 59 69
3 15975 33 15982 37 6001131 14512 62 73
4 16136 35 16143 40 6001138 14730 65 73
pt_r_d pt_r_t pt_r_tt to_id walk_d walk_t GML_ID NAMEFIN \
0 14698 61 72 5975375 14456 207 27517366 Helsinki
1 14661 60 72 5975375 14419 206 27517366 Helsinki
2 14256 55 62 5975375 14014 200 27517366 Helsinki
3 14512 58 70 5975375 14270 204 27517366 Helsinki
4 14730 61 72 5975375 14212 203 27517366 Helsinki
NAMESWE NATCODE geometry
0 Helsingfors 091 POLYGON ((391000.0001349226 6667750.00004299, ...
1 Helsingfors 091 POLYGON ((390750.0001349644 6668000.000042951,...
2 Helsingfors 091 POLYGON ((391000.0001349143 6668000.000042943,...
3 Helsingfors 091 POLYGON ((390750.0001349644 6668000.000042951,...
4 Helsingfors 091 POLYGON ((392500.0001346234 6668000.000042901,...
Nice! Now we have attributes from both layers included.
Let’s see the length of the GeoDataFrame.
In [9]: len(result)
Out[9]: 3836
And the original data.
In [10]: len(grid)
Out[10]: 13231
Let’s save our result grid as a GeoJSON file that is another commonly used file format nowadays for storing spatial data.
resultfp = "/home/geo/data/TravelTimes_to_5975375_RailwayStation_Helsinki.geojson"
# Use GeoJSON driver
result.to_file(resultfp, driver="GeoJSON")
There are many more examples for different types of overlay analysis in Geopandas documentation where you can go and learn more.
Hint
Overlay analysis such as ours with around 13 000 polygons is quite CPU intensive task which can be quite slow to execute. Luckily, doing such analysis in batches improves the performance dramatically (spatial lookups are much quicker that way). The code snippet below shows how to do it with batch size of 10 rows which takes only around 1.5 minutes to run the analysis in our computer instance.
import geopandas as gpd
import numpy as np
# File paths
border_fp = "/home/geo/data/Helsinki_borders.shp"
grid_fp = "/home/geo/data/TravelTimes_to_5975375_RailwayStation.shp"
# Read files
grid = gpd.read_file(grid_fp)
hel = gpd.read_file(border_fp)
# Batch size
b = 10
# Number of iterations (round up with np.ceil) and convert to integer
row_cnt = len(grid)
iterations = int(np.ceil(row_cnt / b))
# Final result
final = gpd.GeoDataFrame()
# Set the start and end index according the batch size
start_idx = 0
end_idx = start_idx + b
for iteration in range(iterations):
print("Iteration: %s/%s" % (iteration, iterations))
# Make an overlay analysis using a subset of the rows
result = gpd.overlay(grid[start_idx:end_idx], hel, how='intersection')
# Append the overlay result to final GeoDataFrame
final = final.append(result)
# Update indices
start_idx += b
end_idx = start_idx + b
# Save the output as GeoJSON
outfp = "/home/geo/data/overlay_analysis_speedtest.geojson"
final.to_file(outfp, driver="GeoJSON")
Aggregating data¶
Aggregating data can also be useful sometimes. What we mean by aggregation is that we basically merge Geometries into together by some common identifier. Suppose we are interested in studying continents, but we only have country-level data like the country dataset. By aggregation we would convert this into a continent-level dataset.
Let’s aggregate our travel time data by car travel times, i.e. the grid cells that have the same travel time to Railway Station will be merged together.
In [11]: result_aggregated = result.dissolve(by="car_r_t")
In [12]: result_aggregated.head()
Out[12]:
geometry car_m_d car_m_t \
car_r_t
-1 (POLYGON ((388000.0001354737 6669000.000042855... -1 -1
0 POLYGON ((386000.0001357812 6672000.000042388,... 0 0
7 POLYGON ((386250.0001357396 6671750.000042424,... 1059 7
8 (POLYGON ((386250.0001357467 6671500.000042468... 1207 8
9 (POLYGON ((387000.0001355996 6671500.000042449... 1768 8
car_r_d from_id pt_m_d pt_m_t pt_m_tt pt_r_d pt_r_t pt_r_tt \
car_r_t
-1 -1 5996387 -1 -1 -1 -1 -1 -1
0 0 5975375 0 0 0 0 0 0
7 1059 5977007 447 6 6 447 6 6
8 1207 5978638 1026 9 11 1026 9 11
9 1768 5980269 1274 11 15 1274 11 15
to_id walk_d walk_t GML_ID NAMEFIN NAMESWE NATCODE
car_r_t
-1 -1 -1 -1 27517366 Helsinki Helsingfors 091
0 5975375 0 0 27517366 Helsinki Helsingfors 091
7 5975375 447 6 27517366 Helsinki Helsingfors 091
8 5975375 774 11 27517366 Helsinki Helsingfors 091
9 5975375 1210 17 27517366 Helsinki Helsingfors 091
Let’s compare the number of cells in the layers before and after the aggregation.
In [13]: len(result)
Out[13]: 3836
In [14]: len(result_aggregated)
��������������Out[14]: 51
Indeed the number of rows in our data has decreased and the Polygons were merged together.
Simplifying geometries¶
Sometimes it might be useful to be able to simplify geometries. This could be something to consider for example when you have very detailed spatial features that cover the whole world. If you make a map that covers the whole world, it is unnecessary to have really detailed geometries because it is simply impossible to see those small details from your map. Furthermore, it takes a long time to actually render a large quantity of features into a map. Here, we will see how it is possible to simplify geometric features in Python by continuing the example from the previous tutorial on data classification.
What we will do next is to only include the big lakes and simplify them slightly so that they are not as detailed.
- Let’s start by reading the lakes data into Geopandas that we saved earlier.
lakes_fp = "/home/geo/lakes.shp"
In [15]: lakes = gpd.read_file(lakes_fp)
- Include only big lakes
In [16]: big_lakes = lakes.ix[lakes['small_big'] == 1].copy()
- Let’s see how they look
In [17]: big_lakes.plot(linewidth=0.05, color='blue');
In [18]: plt.tight_layout()
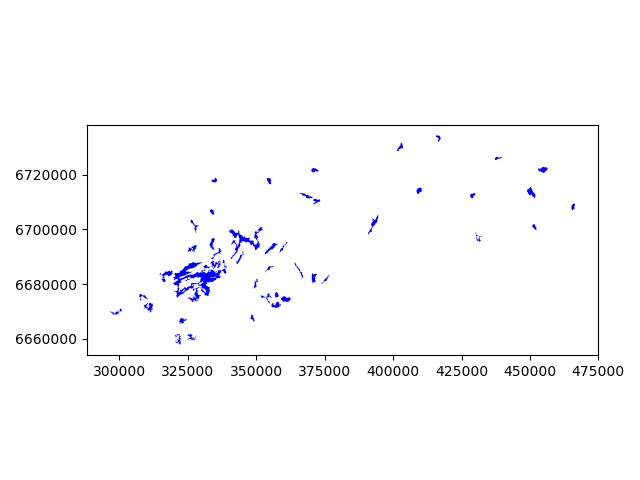
The Polygons that are presented there are quite detailed, let’s generalize them a bit.
- Generalization can be done easily by using a Shapely function called
.simplify(). Thetoleranceparameter is adjusts how much
geometries should be generalized. The tolerance value is tied to the coordinate system of the geometries. Thus, here the value we pass is 300 meters.
In [19]: big_lakes['geom_gen'] = big_lakes.simplify(tolerance=300)
- Let’s set the geometry to be our new column, and plot the results.
In [20]: big_lakes['geometry'] = big_lakes['geom_gen']
In [21]: big_lakes.plot(linewidth=0.05, color='blue')
Out[21]: <matplotlib.axes._subplots.AxesSubplot at 0x2ce1ce29da0>
In [22]: plt.tight_layout()
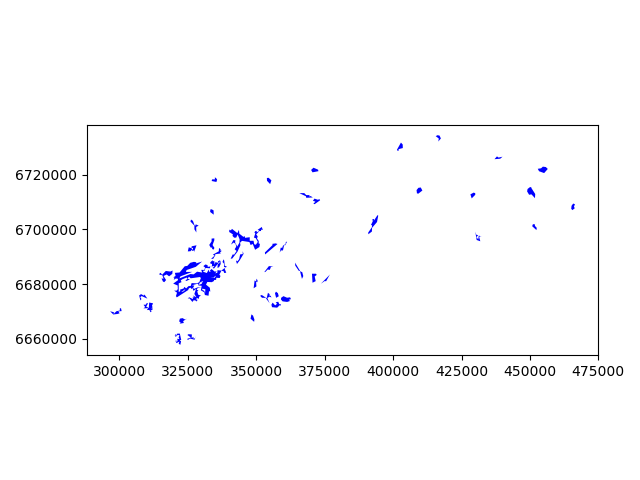
Nice! As a result, now we have simplified our Polygons slightly (although the differences might be a bit hard to spot).